Advertisements
Advertisements
Question
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
Solution
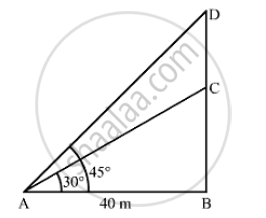
Let BC be the tower and CD be the water tank.
We have,
AB = 40m, ∠BAC = 30° and ∠BAD = 45°
In ΔABD,
` tan 45° = (BD)/(AB)`
`⇒ 1 = (BD)/40`
⇒ BD = 40 M
Now, in Δ ABC
`tan 30° = (BC)/(AB)`
`⇒1/ sqrt(3) = (BC) /40`
`⇒ BC = 40/sqrt(3)`
`⇒ BC = 40/ sqrt(3) xx sqrt(3)/sqrt(3)`
`⇒ BC = (40sqrt(3) )/3 m`
`"(i) The height of the tower," BC = (40 sqrt(3))/3 = (40 xx 1.73)/3 = 23.067 ~~ 23.1 m`
`"(ii) The depth of the tank " CD = (BD - BC) = (40-23.1 ) = 16.9 m`
APPEARS IN
RELATED QUESTIONS
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
