Advertisements
Advertisements
Question
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
Solution
Let h be the height of the light house.
Let us suppose that the distance of one of the ships from the light house is x metres. Then, the distance of the other ship from the light house will be 100 − x metres.
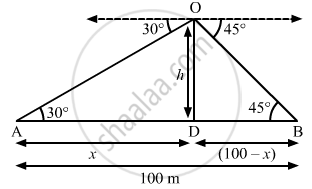
In right-angled triangle ADO, we have:
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{x}\]
\[ \Rightarrow x = \sqrt{3}h . . . (1)\]
\[ \Rightarrow 1 = \frac{h}{100 - x}\]
\[ \Rightarrow x + h = 100\]
\[\text{On putting x} = \sqrt{3}h, \text{we get}: \]
\[\sqrt{3}h + h = 100\]
\[ \Rightarrow h\left( \sqrt{3} + 1 \right) = 100\]
\[ \Rightarrow h = \frac{100}{\sqrt{3} + 1}\]
\[ \Rightarrow h = \frac{100}{\left( \sqrt{3} + 1 \right)} \times \frac{\left( \sqrt{3} - 1 \right)}{\left( \sqrt{3} - 1 \right)}\]
\[ \Rightarrow h = \frac{100}{2}\left( \sqrt{3} - 1 \right)\]
\[ \Rightarrow h = 36 . 6 (\text{approx} . )\]
APPEARS IN
RELATED QUESTIONS
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
