Advertisements
Advertisements
Question
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct upto one place of decimal?
Solution

Given:
Radius (r) of the cylindrical bucket = 18 cm
Height (h) of the cylindrical bucket = 32 cm
Volume of the cylindrical bucket = \[\pi r^2 h\]
\[= \left( \pi \times 18 \times 18 \times 32 \right) {cm}^3\]
Let R be the radius of the conical heap.
Height (H) of the conical heap = 24 cm
Volume of the conical heap =\[\frac{1}{3}\pi R^2 H = \left( \frac{1}{3}\pi R^2 \times 24 \right) {cm}^3 = 8\pi R^2 {cm}^3\]
According to the question:
Volume of the cylindrical bucket = Volume of the conical heap
\[\Rightarrow \pi \times 18 \times 18 \times 32 = 8 \times \pi \times R^2 \]
\[ \Rightarrow R^2 = \frac{18 \times 18 \times 32}{8}\]
\[ = 18\]\[\times\]\[18\]\[\times\]\[4\]\[\]\[\]\[\]\[\]\[\]\[\]\[\]\[\]\[\]\[\]\[\]\[=\]\[1296\]
Let l be the slant height of the conical heap.
\[\therefore l^2 = R^2 + H^2 \]
\[ = {36}^2 + {24}^2 \]
\[ = 1296 + 576\]
\[ = 1872\]
\[ \Rightarrow l = 43 . 3\]
APPEARS IN
RELATED QUESTIONS
A well of diameter 4 m is dug 14 m deep. The earth taken out is spread evenly all around the well to form a 40 cm high embankment. Find the width of the embankment.
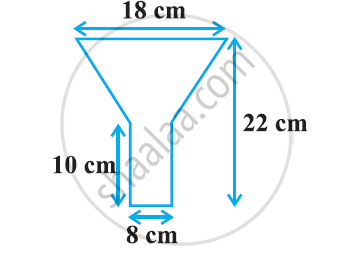
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in level of water in the tank in half an hour ?
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use : π = 355/115)
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
If the length of the diagonal of a cube is `5sqrt(3)` cm, find the total surface area.
Length of the diagonal of the cube = `square`
So, `square` = `5sqrt(3)`
⇒ Side = `square`
Total surface area of cube = `square`
= `square` × `square` × `square`
= `square` cm2
Hence, the total surface area is `square`.
