Advertisements
Advertisements
Question
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
Solution
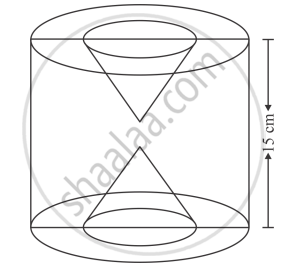
The height of cylinder h = 15 cm
Radius of cylinder \[r = \frac{7}{2}\]
The volume of cylinder
`=pir^2h`
`=pi xx (7/2)^2 xx 15cm^2`
`=183.75 pi`
The radius of conical holes = 3 cm
Height of conical holes = 4 cm.
The volume of conical holes
`=1/3 pir^2h`
`=1/3pi xx 9 xx 4`
`=12 pi cm^3`
Clearly,
The volume of remaining solid
= vol. of cylinder − 2 × vol. of cone
\[= 183 . 75\pi - 24\pi\]
\[ = 501 . 6 {cm}^3\]
APPEARS IN
RELATED QUESTIONS
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (use `pi=22/7`)
Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere ?
No Question.
Water is flowing at the rate of 6 km/hr through a pipe of diameter 14 cm into a rectangular tank which is 60 m long and 22 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
The volumes of two cubes are in the ratio 8 : 27. Find the ratio of their surface areas.
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with a hemisphere tucked at each end. The length of the entire capsule is 2 cm. The capacity of the capsule is
The surface area of a sphere is 154 cm2. The volume of the sphere is
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
The surface areas of two spheres are in the ratio 1 : 2. The ratio of their volume is ______.
A surahi is the combination of ______.
