Advertisements
Advertisements
प्रश्न
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
उत्तर
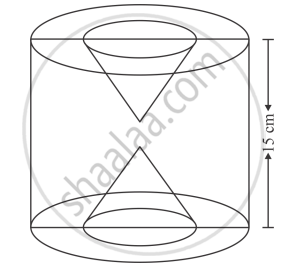
The height of cylinder h = 15 cm
Radius of cylinder \[r = \frac{7}{2}\]
The volume of cylinder
`=pir^2h`
`=pi xx (7/2)^2 xx 15cm^2`
`=183.75 pi`
The radius of conical holes = 3 cm
Height of conical holes = 4 cm.
The volume of conical holes
`=1/3 pir^2h`
`=1/3pi xx 9 xx 4`
`=12 pi cm^3`
Clearly,
The volume of remaining solid
= vol. of cylinder − 2 × vol. of cone
\[= 183 . 75\pi - 24\pi\]
\[ = 501 . 6 {cm}^3\]
संबंधित प्रश्न
A solid metallic sphere of diamter 16 cm is melted and recasted into smaller solid cones, each of radius 4 cm and height 8 cm. Find the number of cones so formed.
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is ______.
A metal parallelopiped of measures 16 cm x 11 cm x 10 cm was melted to make coins. How many coins were made if the thickness and diameter of each coin were 2 mm and 2 cm respectively?
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
The volume of a cube is 729 cm3. Find its surface area.
The volume of a sphere is 4851 cm3. Find its curved surface area.
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used, at the rate of ₹25 per metre.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, then find its height.
