Advertisements
Advertisements
Question
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution
Let the radius of the hemisphere be r units.
Volume of a hemisphere = Surface area of the hemisphere
`=> 2/3 pir^3 = 2pir^2`
`=> 2/3r = 2`
`=> r = 3`
⇒ d = 6 units
Hence, diameter of the hemisphere is equal to 6 units.
APPEARS IN
RELATED QUESTIONS
Water flows at the rate of 15 km/hr through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide . In what time will the level of water in the pond rise by 21 cm.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
The diameters of two circular ends of the bucket are 44 cm and 24 cm . The height of the bucket is 35 cm . The capacity of the bucket is
A spherical glass vessel has a cylindrical neck that is 7 cm long and 4 cm in diameter. The diameter of the spherical part is 21 cm. Find the quantity of water the vessel can hold.
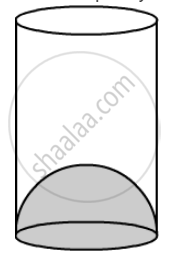
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
Choose the correct answer of the following question:
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.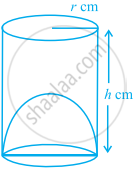
There is a circular pond and a footpath runs along its boundary. A person walks around it, exactly once keeping close to the edge. If his step is 66 cm long and he takes exactly 400 steps to go around the pond, find the diameter of the pond.
