Advertisements
Advertisements
Question
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
Solution
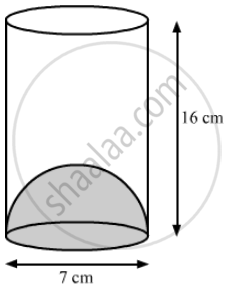
Given the inner diameter of the glass = 7cm
So, the radius of the glass
`"r"=7/2 "cm"` = 3.5 cm
Height of the glass, h = 16 cm and
The volume of the cylindrical glass = πr2h
= `22/7xx7/2xx7/2xx16`
= 616 cm3
Now, radius of the hemisphere = Radius of the cylinder
= r = 3.5 cm
Volume of hemisphere = `2/3`πr3
= `2/3xx22/7xx3.5xx3.5xx3.5`
= 89.83cm3
Now,
Apparent capacity of the glass = Volume of cylinder = 616 cm3
The actual capacity of the glass = Total volume of cylinder - Volume of hemisphere
= 616 - 89.83
= 526.17 cm3
Hence,
Apparent capacity of the glass = 616 cm3
and actual capacity of the glass = 526.17 cm3
APPEARS IN
RELATED QUESTIONS
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
In the middle of a rectangular field measuring 30 m × 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m × 16 m × 11 m.
The volume of a cube is 729 cm3. Find its surface area.
The volume of a sphere is 4851 cm3. Find its curved surface area.
Assertion (A)
The curved surface area of a cone of base radius 3 cm and height 4 cm is 15π cm2.\
Reason (R)
Volume of a cone = πr2h
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The radii of the top and bottom of a bucket of slant height 45cm are 28cm and 7 cm respectively. The curved surface area of the bucket is ______.
A sphere and a cube have equal surface areas. The ratio of the volume of the sphere to that of cube is ______.
What is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
