Advertisements
Advertisements
प्रश्न
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
उत्तर
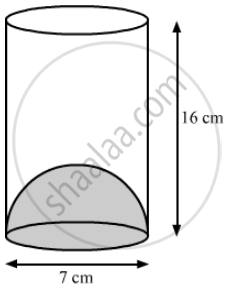
Given the inner diameter of the glass = 7cm
So, the radius of the glass
`"r"=7/2 "cm"` = 3.5 cm
Height of the glass, h = 16 cm and
The volume of the cylindrical glass = πr2h
= `22/7xx7/2xx7/2xx16`
= 616 cm3
Now, radius of the hemisphere = Radius of the cylinder
= r = 3.5 cm
Volume of hemisphere = `2/3`πr3
= `2/3xx22/7xx3.5xx3.5xx3.5`
= 89.83cm3
Now,
Apparent capacity of the glass = Volume of cylinder = 616 cm3
The actual capacity of the glass = Total volume of cylinder - Volume of hemisphere
= 616 - 89.83
= 526.17 cm3
Hence,
Apparent capacity of the glass = 616 cm3
and actual capacity of the glass = 526.17 cm3
APPEARS IN
संबंधित प्रश्न
In Fig. 5, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre `( "Use "pi=22/7)`

A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 `5/9` cm. Find the diameter of the cylindrical vessel.
Choose the correct answer of the following question:
A solid is hemispherical at the bottom and conical (of same radius) above it. If the surface areas of the two parts are equal, then the ratio of its radius and the slant height of the conical part is
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
πThe height of a cylinder is 14 cm and its curved surface area is 264 cm2. The volume of the cylinder is
If the radii of the ends of a bucket are 5 cm and 15 cm and it is 24 cm high, then its surface area is
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The slant height of the frustum of a cone is 4 cm and the perimeters (i.e. circumferences) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.

In Figure 3, a decorative block is shown which is made of two solids, a cube, and a hemisphere. The base of the block is a cube with an edge 6 cm and the hemisphere fixed on the top has a diameter of 4⋅2 cm. Find
(a) the total surface area of the block.
(b) the volume of the block formed. `("Take" pi = 22/7)`
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
