Advertisements
Advertisements
प्रश्न
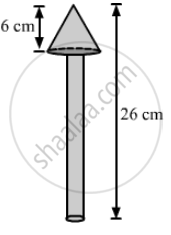
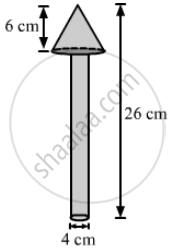
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
Advertisements
उत्तर
we have,
the base radius of the conical part, r = 5/2= 2.5 cm,
the base radius of the cylindrical part, R = 4/2 = 2 cm
the total height of the toy = 26 cm,
the height of the conical part, h = 6 cm
Also, the height of the cylindrical part , H=26-6 = 20 cm
And, the slant height of the conical part, `l = sqrt(r^2+ h^2) = sqrt (2.5^2+6^2) = sqrt(6.25+36)=sqrt(42.25) = 6.5 cm `
Now,
The area to be painted by red colour = CSA of cone + Area of base of conical part -Area base of cylinderical part
`= pirl+pir^2-piR^2`
`= 22/7xx2.5xx6.5+22/7xx2.5xx2.5-22/7xx2xx2`
`=22/7xx 16.25 +22/7xx6.25- 22/7xx4`
`= 22/7xx(16.25+6.25-4)`
`=22/7xx18.5`
≈ 58.14 cm2
Also,
The area to be painted by white colour = CSA of cylinder + Area of base of cylinder
`= 2piRH + piR^2`
`=piR(2H+R)`
`=22/7xx2xx(2xx20+2)`
`=22/7xx2xx42`
= 264 cm2
APPEARS IN
संबंधित प्रश्न
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
If the radii of circular ends of a bucket 24cm high are 5cm and 15cm. find surface area of
bucket?
The radii of the circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and the volume of the frustum.
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 10459 `3/7` cm3. The radii of its lower and upper circular ends are 8cm and 20cm. find the cost of metal sheet used in making container at rate of Rs 1.4 per cm2?
Find the number of metallic circular discs with a 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
A copper wire of diameter 6 mm is evenly wrapped on a cylinder of length 18 cm and diameter 49 cm to cover its whole surface. Find the length and the volume of the wire. If the density of the copper be 8.8 g per cm3, then find the weight of the wire.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
3 cubes each of 8 cm edge are joined end to end. Find the total surface area of the cuboid.
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.
