Advertisements
Advertisements
प्रश्न
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
उत्तर
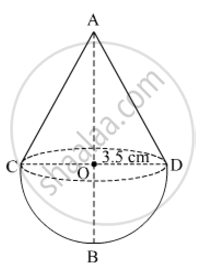
Let r and h be the radius and height of the cone mounted on the hemisphere, respectively.
Suppose R be the radius of the hemishpere.
Now,
r = R = 3.5 cm
Height of the cone + Radius of the hemisphere = Total height of the toy
∴ h + 3.5 cm = 15.5 cm
⇒ h = 15.5 − 3.5 = 12 cm
Let l be the slant height of the cone.
∴l2=r2+h2
`=>l^2=(7/2)^2+(12)^2=49/4+144=625/4`
`=>l = 25/2cm`
Total surface area of the toy
= Curved surface area of the cone + Curved surface area of the hemisphere
=πrl+2πr2
=πr(l+2r)
`=22/7xx7/2xx(25/2+2xx7/2)`
`=22/7xx7/2xx39/2`
=214.5 cm2
APPEARS IN
संबंधित प्रश्न
If the total surface area of a solid hemisphere is 462 cm2 , find its volume.[Take π=22/7]
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemi-spherical end is 0.7 m.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
