Advertisements
Advertisements
प्रश्न
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
Advertisements
उत्तर
(a)
Let R and r be the top and base of the bucket and let h be its height.
Then, R = 20 cm, r = 10 cm and h = 30 cm.
Capacity of the bucket = Volume of the frustum of the cone
`= (pi"h")/3("R"^2 + "r"^2 + "Rr")`
`= 22/7xx1/3xx30xx[(20)^2 + (10^2) + (20xx10)] "cm"^3`
`= 22/7xx[400+100+200]"cm"^3`
`=(220/7xx700)"cm"^3`
= 22000 cm3
Hence, (a) ⇒ (q)
(b)
Let R and r be the top and base of the bucket and let h be its height.
Then, R = 20 cm, r = 12 cm and h = 15 cm
`"Slant height of the bucket" "l" = sqrt(h^2 + ("R"-r)^2) `
`=sqrt((15)^2 + (20-12)^2)`
`=sqrt(225+64)`
`=sqrt(289) `
= 17 cm
Hence, (b) ⇒ (s)
(c)
Let R and r be the top and base of the bucket and let be its slant height.
Then, R = 33 cm, r = 27 cm and h = 10 cm
Total surface area of the bucket `= pi ["R"^2 +"r"^2+"l"("R" + r)]`
`= pixx[(33)^2 + (27)^2 + 10xx(33+27)]`
`= pi xx [1089 + 729 + 600]`
`= 2418pi "cm"^2`
Hence, (c) ⇒ (p)
(d)
Let the diameter of the required sphere be d.
Then, volume of the sphere`=4/3 pi"r"^3`
`= 4/3pi("d"/2)^3`
Therefore,
`4/3pi("d"/2)^3 = 4/3pi(3)^3 + 4/3pi(4)^3 + 4/3pi(5)^3`
`=> 4/3pi"d"^3/8 = 4/3pixx[(3)^3+(4)^3 + (5)^3`
`= "d"^3/8 = 216`
⇒ d3 = 1728
⇒ d3 = 123
⇒ d = 12 cm
Hence, (d) ⇒ (r)
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(q) 22000 |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
((s) 17 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(p) 2418π |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(r) 12 |
APPEARS IN
संबंधित प्रश्न
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
If the radii of circular ends of a bucket 24cm high are 5cm and 15cm. find surface area of
bucket?
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. [User `pi22/7`]
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2 .
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
A hemispherical bowl of internal diameter 30 cm contains some liquid. This liquid is to be poured into cylindrical bottles of diameter 5 cm and height 6 cm each. Find the number of bottles required.
A plumbline (sahul) is a combination of
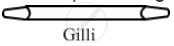
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere and hence find the surface area of this sphere.
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
|
Khurja is a city in the Indian state of Uttar Pradesh famous for the pottery. Khurja pottery is traditional Indian pottery work which has attracted Indians as well as foreigners with a variety of tea sets, crockery and ceramic tile works. A huge portion of the ceramics used in the country is supplied by Khurja and is also referred as "The Ceramic Town". One of the private schools of Bulandshahr organised an Educational Tour for class 10 students to Khurja. Students were very excited about the trip. Following are the few pottery objects of Khurja.
Students found the shapes of the objects very interesting and they could easily relate them with mathematical shapes viz sphere, hemisphere, cylinder etc. |
Maths teacher who was accompanying the students asked the following questions:
- The internal radius of hemispherical bowl (filled completely with water) in I is 9 cm and the radius and height of the cylindrical jar in II are 1.5 cm and 4 cm respectively. If the hemispherical bowl is to be emptied in cylindrical jars, then how many cylindrical jars are required?
- If in the cylindrical jar full of water, a conical funnel of the same height and same diameter is immersed, then how much water will flow out of the jar?
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.
