Advertisements
Advertisements
प्रश्न
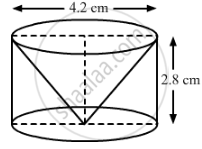
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
उत्तर
The following figure shows the required cylinder and the conical cavity.
Given:
Height (h) of the conical part = Height (h) of the cylindrical part = 2.8 cm
Diameter of the cylindrical part = Diameter of the conical part = 4.2 cm
∴ Radius (r) of the cylindrical part = Radius (r) of the conical part = 2.1 cm
Slant height (l) of the conical part `=sqrt(r^2+h^2)`
`=sqrt((2.1)^2+(2.8)^2)cm`
`=sqrt(4.41+7.84)cm`
`=sqrt(12.25)cm=3.5 cm`
Total surface area of the remaining solid = Curved surface area of the cylindrical part + Curved surface area of the conical part + Area of the cylindrical base
`=2pirh+pirl+pir^2`
`=(2xx22/7xx2.1xx2.8+22/7xx2.1xx3.5+22/7xx2.1xx2.1) cm^2`
`=(36.96+23.1+13.86)cm^2`
`=73.92 cm^2`
Thus, the total surface area of the remaining solid is 73.92 cm2.
APPEARS IN
संबंधित प्रश्न
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is ______.

Two cubes each of volume 8 cm³ are joined end to end, then the surface area of the resulting cuboid is ______.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
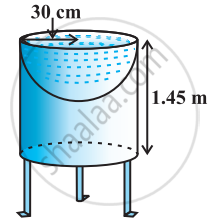
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.