Advertisements
Advertisements
प्रश्न
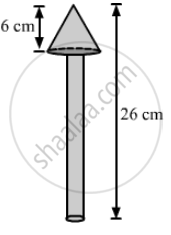
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
उत्तर
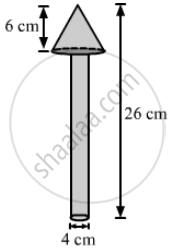
we have,
the base radius of the conical part, r = 5/2= 2.5 cm,
the base radius of the cylindrical part, R = 4/2 = 2 cm
the total height of the toy = 26 cm,
the height of the conical part, h = 6 cm
Also, the height of the cylindrical part , H=26-6 = 20 cm
And, the slant height of the conical part, `l = sqrt(r^2+ h^2) = sqrt (2.5^2+6^2) = sqrt(6.25+36)=sqrt(42.25) = 6.5 cm `
Now,
The area to be painted by red colour = CSA of cone + Area of base of conical part -Area base of cylinderical part
`= pirl+pir^2-piR^2`
`= 22/7xx2.5xx6.5+22/7xx2.5xx2.5-22/7xx2xx2`
`=22/7xx 16.25 +22/7xx6.25- 22/7xx4`
`= 22/7xx(16.25+6.25-4)`
`=22/7xx18.5`
≈ 58.14 cm2
Also,
The area to be painted by white colour = CSA of cylinder + Area of base of cylinder
`= 2piRH + piR^2`
`=piR(2H+R)`
`=22/7xx2xx(2xx20+2)`
`=22/7xx2xx42`
= 264 cm2
APPEARS IN
संबंधित प्रश्न
If the total surface area of a solid hemisphere is 462 cm2 , find its volume.[Take π=22/7]
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy [Use π =`22/7`]
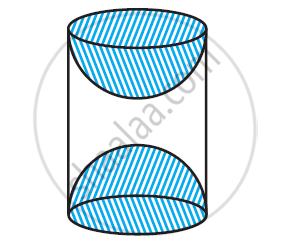
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
A bucket made of aluminum sheet is of height 20cm and its upper and lower ends are of radius 25cm an 10cm, find cost of making bucket if the aluminum sheet costs Rs 70 per
100 cm2
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
A plumbline (sahul) is the combination of (see figure) ______.