Advertisements
Advertisements
प्रश्न
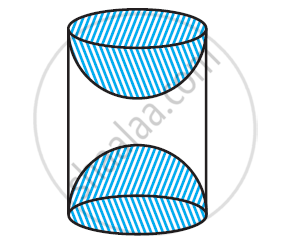
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
उत्तर
Given that,
Radius (r) of cylindrical part = Radius (r) of hemispherical part = 3.5 cm
Height of cylindrical part (h) = 10 cm
Surface area of article = CSA of cylindrical part + 2 × CSA of hemispherical part
= 2πrh + 2 × 2πr2
= 2π × 3.5 × 10 + 2 × 2π × 3.5 × 3.5
= 70π + 49π
= 119π
= 17 × 22
= 374 cm2
APPEARS IN
संबंधित प्रश्न
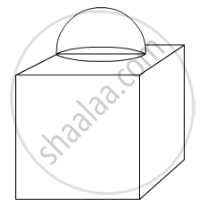
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
The internal and external diameters of a hollow hemisphere vessel are 21cm and 25.2 cm The cost of painting 1cm2 of the surface is 10paise. Find total cost to paint the vessel all
over______?
A tent of height 77dm is in the form a right circular cylinder of diameter 36m and height 44dm surmounted by a right circular cone. Find the cost of canvas at Rs.3.50 per m2 ?
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm. and 6 cm, respectively. Find the total surface area of the solid. (Use π =`22/7`)
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. [User `pi22/7`]
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemi-spherical end is 0.7 m.
The volume of a hemisphere is 2425 `1/2` cm3 . Find its curved surface area.
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
Five identical cubes, each of edge 5 cm, are placed adjacent to each other. Find the volume of the resulting cuboid.
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
If the volumes of a cube is 1728 cm³, the length of its edge is equal to ______.
Tamper-proof tetra-packed milk guarantees both freshness and security. This milk ensures uncompromised quality, preserving the nutritional values within and making it a reliable choice for health-conscious individuals.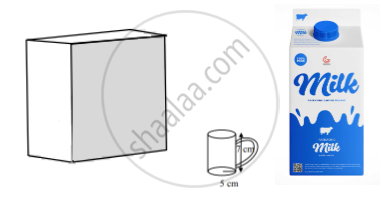
500 ml milk is packed in a cuboidal container of dimensions 15 cm × 8 cm × 5 cm. These milk packets are then packed in cuboidal cartons of dimensions 30 cm × 32 cm × 15 cm.
Based on the above-given information, answer the following questions:
i. Find the volume of the cuboidal carton. (1)
ii. a. Find the total surface area of the milk packet. (2)
OR
b. How many milk packets can be filled in a carton? (2)
iii. How much milk can the cup (as shown in the figure) hold? (1)
