Advertisements
Advertisements
प्रश्न
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
उत्तर
The radii of the top and bottom circles are r1 = 20 cm and r2 = 10 cm respectively. The height of the bucket is h= 12 cm. Therefore, the volume of the bucket is
`V=1/3pi(r_1^2+r_1r_2+r_2^2)xxh`
`=1/3pi(20^2+20xx10+10^2)xx12`
`=1/3xx22/7xx700xx12`
= 8800 cm3
The slant height of the bucket is
`l=sqrt((r_1-r_2)^2+h^2)`
`=sqrt((20+10)^2+12^2)`
`=sqrt(244)`
`=2sqrt(61) cm`
The total surface area of the bucket is
`=pi(r_1-r_2)xxl+pir_2^2`
`=22/7xx(20+10)xx2sqrt(61)+22/7xx10^2`
`=(1320sqrt(61)+2200)/7xxcm^2`
`=(1320sqrt(61)+2200)/7xx100 dm^2`
The total cost of tin sheet used for making the bucket is
`=1.20xx((1320sqrt(61)+2200)/(7xx100))`
= 21.40
APPEARS IN
संबंधित प्रश्न
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm. [Use π = 3.14]
A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone. (use π 3.14).
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
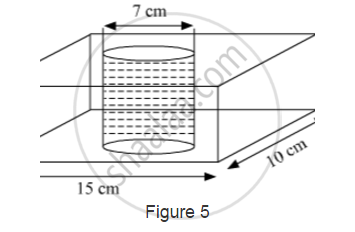
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2 .
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is ______.

