Advertisements
Advertisements
प्रश्न
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
उत्तर
The radii of the bottom and top circles are r1 = 10 cm and r2 = 6 cm respectively. The height of the frustum cone is h= 3 cm. Therefore, the volume of the bucket is
`V=1/3pi(r_1^2+r_1r_2+r_2^2)xxh`
`=1/3pi(10^2+10xx6+6^2)xx3`
= 616 cm3
Hence Volume = 616 cm3
The slant height of the bucket is
`l=sqrt((r_1-r_2)+h^2)`
`=sqrt((10-6)^2+3^2)`
`=sqrt(25)`
= 5cm
The total surface area of the frustum cone is
`pi(r_1+r_2)xxl+pir_1_pir_2^2`
`=22/7xx(10+6)xx5+22/7xx10^2+22/7xx6^2`
`=4752/7`Square cm
= 678.85 Square cm
Hence Total surface area = 678.85
APPEARS IN
संबंधित प्रश्न
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
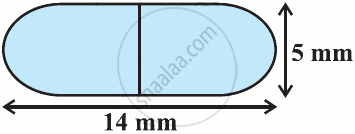
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
If the radii of circular ends of a bucket 24cm high are 5cm and 15cm. find surface area of
bucket?
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
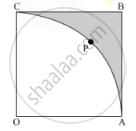
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
