Advertisements
Advertisements
प्रश्न
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
उत्तर
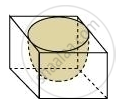
Diameter of hemisphere = Edge of cube = l
Radius of hemisphere = `l/2`
Curved surface area of hemisphere = 2πr2
= `2 xx pi xx l/2 xxl/2 xx (pi l^2)/2`
Base area of the hemisphare = πr2
= `pi (l/2)^2 = (pil^2)/4`
Surface area of the cube = `6 xx l^2 = 6l^2`
Surface area of the remaining solid = [Total surface area of cube + C.S.A. of hemispjere − base area of hemisphere]
= `6l^2 + (pil^2)/2 − (pil^2)/2`
= `(24l^2 + 2pil^2 − pil^2)/4`
= `(24l^2 + pil^2)/4`
= `l^2/4 (24 + pi)` sq. units.
APPEARS IN
संबंधित प्रश्न
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
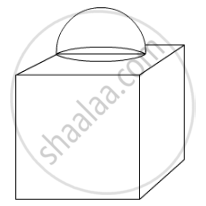
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid. [Use `pi = 22/7`]
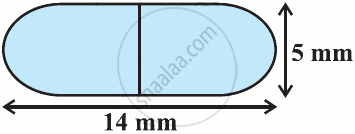
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
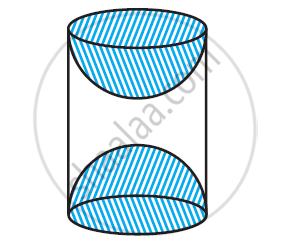
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
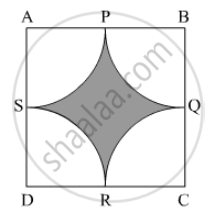
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
Radii of circular ends of a solid frustum off a cone re 33cm and 27cm and its slant height are 10cm. find its total surface area?
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
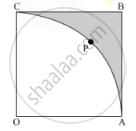
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
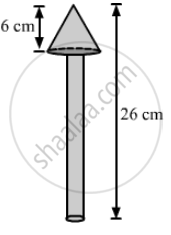
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
A copper wire of diameter 6 mm is evenly wrapped on a cylinder of length 18 cm and diameter 49 cm to cover its whole surface. Find the length and the volume of the wire. If the density of the copper be 8.8 g per cm3, then find the weight of the wire.
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
A plumbline (sahul) is the combination of (see figure) ______.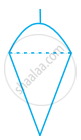
The shape of a gilli, in the gilli-danda game (see figure), is a combination of ______.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
Tamper-proof tetra-packed milk guarantees both freshness and security. This milk ensures uncompromised quality, preserving the nutritional values within and making it a reliable choice for health-conscious individuals.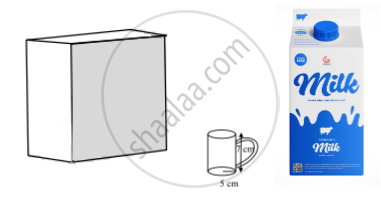
500 ml milk is packed in a cuboidal container of dimensions 15 cm × 8 cm × 5 cm. These milk packets are then packed in cuboidal cartons of dimensions 30 cm × 32 cm × 15 cm.
Based on the above-given information, answer the following questions:
i. Find the volume of the cuboidal carton. (1)
ii. a. Find the total surface area of the milk packet. (2)
OR
b. How many milk packets can be filled in a carton? (2)
iii. How much milk can the cup (as shown in the figure) hold? (1)
