Advertisements
Advertisements
प्रश्न
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
उत्तर
Given that,
Volume of cubes = 64 cm3
(Edge)3 = 64
Edge = 4 cm
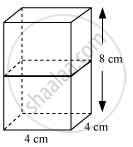
If cubes are joined end to end, the dimensions of the resulting cuboid will be 4 cm, 4 cm, 8 cm.
∴ Surface area of cuboids = 2(lb + bh + lh)
= 2[(4 × 4) + (4 × 8) + (4 × 8)]
= 2(16 + 32 + 32)
= 2(16 + 64)
= 2 × 80
= 160 cm2.
APPEARS IN
संबंधित प्रश्न
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
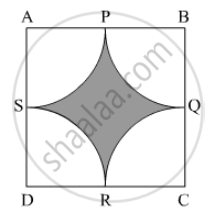
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
Prove that the surface area of a sphere is equal to the curved surface area of the circumference cylinder__?
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
The radii of the circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and the volume of the frustum.
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
A copper wire of diameter 6 mm is evenly wrapped on a cylinder of length 18 cm and diameter 49 cm to cover its whole surface. Find the length and the volume of the wire. If the density of the copper be 8.8 g per cm3, then find the weight of the wire.
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
The shape of the gilli used in a gilli-danda game is a combination of
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
Eight solid sphere of same size are made by melting a solid metallic cylinder of base diameter 6 cm and height 32 cm. The diameter of each sphere is ______.
3 cubes each of 8 cm edge are joined end to end. Find the total surface area of the cuboid.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.
