Advertisements
Advertisements
प्रश्न
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
उत्तर
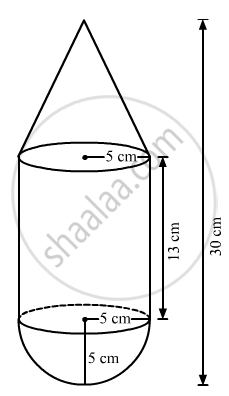
S1 = 2π(2)(13)
S1 =408.2cm2
Curved surface area of cone(S1) = πrl
Let l be slant height of cone
`l=sqrt(r^2+h^2`
h = 30 - 13 - 5 = 12cm
⇒`l=sqrt(12^2+5^2)` = 13cm
l = 13cm
∴Curved surface area of cone(S2) = π(5)(13)
= 204.1cm2
Curved surface area of hemisphere(S3) = 2πr2
= 2π(5)2
= 2π(25) = 50π = 157cm2
Total curved surface area(S) = S1 + S2 + S3
S = 408.2 + 204.1 + 157
S = 769.3cm2
∴ Surface area of toy(S) = 769.3cm2
APPEARS IN
संबंधित प्रश्न
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [Use π=22/7]
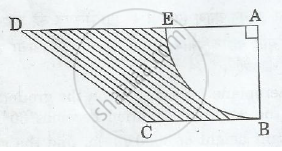
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
The radii of the circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and the volume of the frustum.
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimension 6cm \[\times\] 42cm \[\times\] 21 cm.
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
