Advertisements
Advertisements
Question
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
Solution
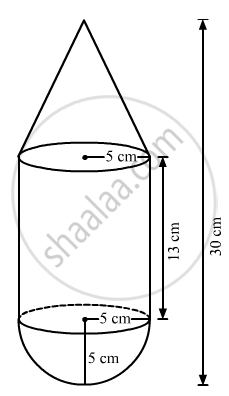
S1 = 2π(2)(13)
S1 =408.2cm2
Curved surface area of cone(S1) = πrl
Let l be slant height of cone
`l=sqrt(r^2+h^2`
h = 30 - 13 - 5 = 12cm
⇒`l=sqrt(12^2+5^2)` = 13cm
l = 13cm
∴Curved surface area of cone(S2) = π(5)(13)
= 204.1cm2
Curved surface area of hemisphere(S3) = 2πr2
= 2π(5)2
= 2π(25) = 50π = 157cm2
Total curved surface area(S) = S1 + S2 + S3
S = 408.2 + 204.1 + 157
S = 769.3cm2
∴ Surface area of toy(S) = 769.3cm2
APPEARS IN
RELATED QUESTIONS
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
The internal and external diameters of a hollow hemisphere vessel are 21cm and 25.2 cm The cost of painting 1cm2 of the surface is 10paise. Find total cost to paint the vessel all
over______?
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 10459 `3/7` cm3. The radii of its lower and upper circular ends are 8cm and 20cm. find the cost of metal sheet used in making container at rate of Rs 1.4 per cm2?
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
If the volumes of a cube is 1728 cm³, the length of its edge is equal to ______.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
