Advertisements
Advertisements
Question
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub (Take π = 22/7)
Solution
To find the volume of the water left in the tube, we have to subtract the volume of the hemisphere and cone from volume of the cylinder.
For right circular cylinder, we have
r = 5cm
h = 9.8 cm
The volume of the cylinder is
V1 = πr2h
`=22/7xx5^2xx9.8`
= 770cm
For hemisphere and cone, we have
r = 3.5 cm
h = 5 cm
Therefore the total volume of the cone and hemisphere is
`V_2=1/3pir^2h+2/3pir^3`
`=1/3xx22/7xx3.5^2xx5+2/3xx22/7xx3.5^3`
= 154 cm3
The volume of the water left in the tube is
V = V1 - V2
Hence, the volume of the water left in the tube is V = 616cm3
APPEARS IN
RELATED QUESTIONS
An iron spherical ball has been melted and recast into smaller balls of equal size. If the radius of each of the smaller balls is 1/4 of the radius of the original ball, how many such balls are made? Compare the surface area, of all the smaller balls combined together with that of the original ball.
A copper sphere of radius 3cm is melted and recast into a right circular cone of height 3cm.find radius of base of cone?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A solid consists of a circular cylinder surmounted by a right circular cone. The height of the cone is h. If the total height of the solid is 3 times the volume of the cone, then the height of the cylinder is
Choose the correct answer of the following question:
A metallic solid sphere of radius 9 cm is melted to form a solid cylinder of radius 9 cm. The height of the cylinder is
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
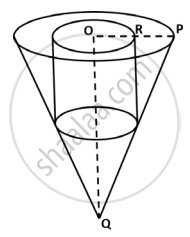
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)