Advertisements
Advertisements
Question
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
Solution
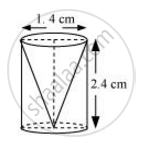
Given that,
Height (h) of the conical part = Height (h) of the cylindrical part = 2.4 cm
Diameter of the cylindrical part = 1.4 cm
Therefore, radius (r) of the cylindrical part = 0.7 cm
Slant height (l) of conical part =` sqrt(r^2 + h^2)`
`= sqrt((0.7)^2+(2.4)^2) `
`=sqrt(0.49+5.76)`
`=sqrt(6.25)`
= 2.5
Total surface area of the remaining solid will be = CSA of cylindrical part + CSA of conical part + Area of cylindrical base
= 2πrh + πrl + πr2
`= 2xx 22/7xx 0.7xx2.4+22/7xx0.7xx2.5+22/7xx0.7xx0.7`
= `4.4 xx 2.4 + 2.2 xx 2.5 + 2.2 xx 0.7`
= 10.56 + 5.50 +1.54
= 17.60 cm2
The total surface area of the remaining solid to the nearest cm2 is 18 cm2.
APPEARS IN
RELATED QUESTIONS
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
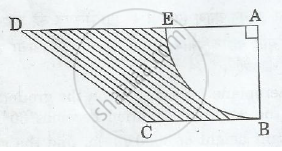
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone. (use π 3.14).
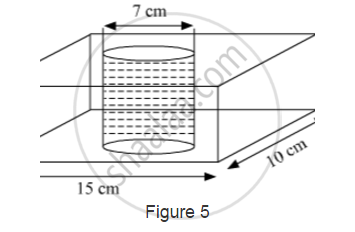
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
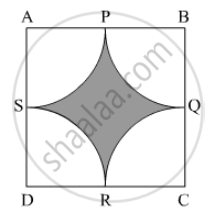
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm .
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere and hence find the surface area of this sphere.
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
The total surface area of a solid hemisphere of radius r is ________.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
The total surface area of a solid hemisphere of radius 7 cm is ______.
