Advertisements
Advertisements
Question
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
Solution
We have,
the internal radius of the cylindrical pipe, r = 2/2 = 1 cm and
the base radius of cylindrical tank, R = 40 cm.
Also, the rate of flow, h = 0.4 m/s = 40 cm/s
Let the rise in level of water be H.
Now,
The volume of water flowing out of the cylindrical pipe in 1 sec =πr2h = π × 1 × 1 × 40 = 40π cm3
As,
Volume of water in the cylindrical tank = Volume of standing water in cylindrical pipe
⇒πR2H = 72000π
⇒R^2H = 72000`
⇒ 40 × 40 × H = 7200H
`rArr H = 72000/(40xx40)`
∴ H = 45 cm
So, the rise in level of water in the tank in half an hour is 45 cm.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
RELATED QUESTIONS
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
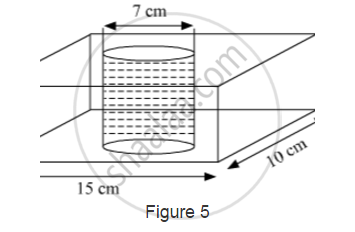
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A tent of height 77dm is in the form a right circular cylinder of diameter 36m and height 44dm surmounted by a right circular cone. Find the cost of canvas at Rs.3.50 per m2 ?
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]

The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
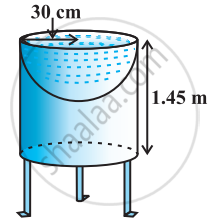
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.