Advertisements
Advertisements
प्रश्न
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
Advertisements
उत्तर
We have,
the internal radius of the cylindrical pipe, r = 2/2 = 1 cm and
the base radius of cylindrical tank, R = 40 cm.
Also, the rate of flow, h = 0.4 m/s = 40 cm/s
Let the rise in level of water be H.
Now,
The volume of water flowing out of the cylindrical pipe in 1 sec =πr2h = π × 1 × 1 × 40 = 40π cm3
As,
Volume of water in the cylindrical tank = Volume of standing water in cylindrical pipe
⇒πR2H = 72000π
⇒R^2H = 72000`
⇒ 40 × 40 × H = 7200H
`rArr H = 72000/(40xx40)`
∴ H = 45 cm
So, the rise in level of water in the tank in half an hour is 45 cm.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
संबंधित प्रश्न
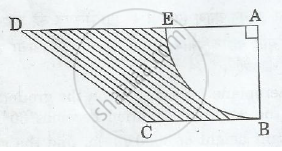
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. `("use " pi=22/7)`
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
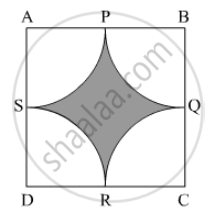
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. [User `pi22/7`]
Find the number of metallic circular discs with a 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
The volume of a hemisphere is 2425 `1/2` cm3 . Find its curved surface area.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
A plumbline (sahul) is the combination of (see figure) ______.
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.
Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.
The ratio of total surface area of a solid hemisphere to the square of its radius is ______.
