Advertisements
Advertisements
प्रश्न
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
उत्तर
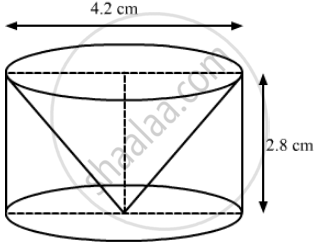
We have,
the height of the cone = the height of the cylinder = h =2.8 cm and the radius of the base, r = `4.2/2 = 2.1 "cm"`
The slant height of the cone, `l = sqrt(r^2 + h^2)`
`=sqrt(2.1^2 + 2.8^2)`
`= sqrt(4.41 +7.84)`
`=sqrt(12.25)`
= 3.5 cm
Now, the total surface area of the remaining solid = CSA of cylinder + CSA of cone + Area of base
`= 2pirh + pirl + pir^2`
`=pir (2h +l +r)`
`= 22/7 xx2.1xx(2xx2.8xx3.5+2.1)`
`= 22xx0.3xx(5.6+5.6)`
`=6.6xx 11.2`
`= 73.92 "cm"^2`
So, the total surface area of the remaining solid is 73.92 cm2.
APPEARS IN
संबंधित प्रश्न
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
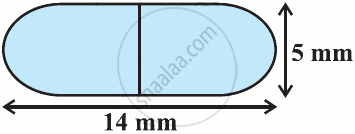
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
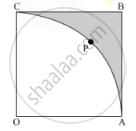
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of these balls are 1.5 cm and 2 cm. Find the radius of the third ball.
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere and hence find the surface area of this sphere.
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.
