Advertisements
Advertisements
प्रश्न
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of these balls are 1.5 cm and 2 cm. Find the radius of the third ball.
उत्तर
Radius of sphere = 3 cm
Radius of first ball = 1.5 cm
Radius of second ball = 2 cm
Radius of second ball = 2 cm
`=4/3pixx3^3 -(4/3pixx3^3/2+4/3pixx2^3)`
`=4/3pixx3xx3xx3 - (4/3pixx3/2xx3/2xx3/2+4/3pixx2xx2xx2)`
`=4pixx3xx3-(pixx(3xx3)/2 + 4/3pixx2xx2xx2)`
`=36pi - (pi9/2+32/3pi)`
`=((36xx6-9xx3-32xx2)/6)pi `
`=((216-27-64)/6)pi =(125pi)/6`
Therefore,
`4/3pir^3 = (125pi)/6`
`Or, r = root(3)((125xx3)/(4xx6)) = root(3)(125/8) = 5/2 = 2.5 "cm"`
APPEARS IN
संबंधित प्रश्न
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm. [Use π = 3.14]
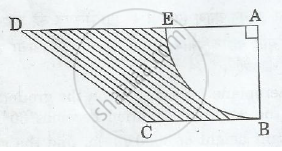
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
A bucket made of aluminum sheet is of height 20cm and its upper and lower ends are of radius 25cm an 10cm, find cost of making bucket if the aluminum sheet costs Rs 70 per
100 cm2
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
A hemispherical bowl of internal diameter 30 cm contains some liquid. This liquid is to be poured into cylindrical bottles of diameter 5 cm and height 6 cm each. Find the number of bottles required.
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
