Advertisements
Advertisements
प्रश्न
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
उत्तर १
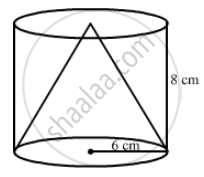
Volume of the solid left = Volume of cylinder - Volume of cone `=pir^2h - 1/3pir^2h = 2/3 xx 22/7 xx 8 xx 6 xx 6 = 603.428 "cm^3'`
The slant length of the cone , `l =sqrt(r^2 + h^2) = sqrt(36+64) = 10 "cm"`
Total surface area of final solid = Area of base circle
उत्तर २

Volume of the solid left = Volume of cylinder - Volume of cone `=pir^2h - 1/3pir^2h = 2/3 xx 22/7 xx 8 xx 6 xx 6 = 603.428 "cm^3'`
The slant length of the cone ,`l =sqrt(r^2 + h^2) = sqrt(36+64) = 10 "cm"`
Total surface area of final solid = Area of base circle + Curved surface area of cylinder +curved area of once`= pirl^2 + 2pirh + pirl = pir (r + 2h +l) = 22/7 xx 6 xx (6 + 16 + 10) = 603.42 "cm"^2`
APPEARS IN
संबंधित प्रश्न
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond ?
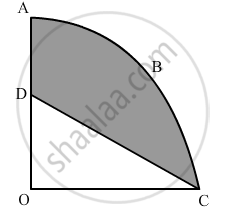
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4, what is the ratio of their volumes?
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
πThe height of a cylinder is 14 cm and its curved surface area is 264 cm2. The volume of the cylinder is
Assertion (A)
If the radii of the circular ends of a bucket 24 cm high are 15 cm and 5 cm, respectively, then the surface area of the bucket is 545π cm2.
- Reason(R)
If the radii of the circular ends of the frustum of a cone are R and r, respectively, and its height is h, then its surface area is - Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
In a right circular cone, if the perpendicular height is 12 cm and the radius is 5 cm, then find its slant height.
What is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
