Advertisements
Advertisements
Question
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
Solution 1
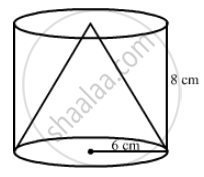
Volume of the solid left = Volume of cylinder - Volume of cone `=pir^2h - 1/3pir^2h = 2/3 xx 22/7 xx 8 xx 6 xx 6 = 603.428 "cm^3'`
The slant length of the cone , `l =sqrt(r^2 + h^2) = sqrt(36+64) = 10 "cm"`
Total surface area of final solid = Area of base circle
Solution 2

Volume of the solid left = Volume of cylinder - Volume of cone `=pir^2h - 1/3pir^2h = 2/3 xx 22/7 xx 8 xx 6 xx 6 = 603.428 "cm^3'`
The slant length of the cone ,`l =sqrt(r^2 + h^2) = sqrt(36+64) = 10 "cm"`
Total surface area of final solid = Area of base circle + Curved surface area of cylinder +curved area of once`= pirl^2 + 2pirh + pirl = pir (r + 2h +l) = 22/7 xx 6 xx (6 + 16 + 10) = 603.42 "cm"^2`
APPEARS IN
RELATED QUESTIONS
The dimensions of a solid iron cuboid are 4·4 m × 2·6 m × 1·0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
The radii of two cones are in the ratio 2 : 1 and their volumes are equal. What is the ratio of their heights?
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \[\frac{1}{27}\] of the volume of the given cone, then the height above the base at which the section has been made, is
A solid metallic spherical ball of diameter 6 cm is melted and recast into a cone with diameter of the base as 12 cm. The height of the cone is
A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder. The diameter of the hemisphere is 21 cm and the total height of the vessel is 14.5 cm. Find its capacity.
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
How many solid cylinders of radius 6 cm and height 12 cm can be made by melting a solid sphere of radius 18 cm?
Activity: Radius of the sphere, r = 18 cm
For cylinder, radius R = 6 cm, height H = 12 cm
∴ Number of cylinders can be made =`"Volume of the sphere"/square`
`= (4/3 pir^3)/square`
`= (4/3 xx 18 xx 18 xx 18)/square`
= `square`
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
Four horses are tethered with equal ropes at 4 corners of a square field of side 70 metres so that they just can reach one another. Find the area left ungrazed by the horses.
