Advertisements
Advertisements
प्रश्न
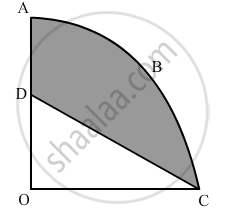
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
उत्तर
Area of the quadrant OABC\[= \frac{1}{4} \times \pi r^2\]\[= \left( \frac{1}{4} \times \frac{22}{7} \times 7 \times 7 \right) {cm}^2 \]
\[ = \frac{77}{2} {cm}^2\]
Area of ΔODC\[=\]\[\frac{1}{2} \times OD \times OC\]
\[= \left( \frac{1}{2} \times 4 \times 7 \right) {cm}^2 ( \because \text{OC is the radius of the circle})\]
\[ = 14 {cm}^2\]
Area of the shaded region = Area of the quadrant OABC − Area of ΔODC
\[= \frac{77}{2} {cm}^2 - 14 {cm}^2 \]
\[ = \frac{77 - 28}{2} {cm}^2 \]
\[ = \frac{49}{2} {cm}^2 \]
\[ = 24 . 5 {cm}^2 \]
APPEARS IN
संबंधित प्रश्न
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
A solid metallic sphere of diamter 16 cm is melted and recasted into smaller solid cones, each of radius 4 cm and height 8 cm. Find the number of cones so formed.
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is ______.
Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in level of water in the tank in half an hour ?
Find the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
The slant height of a bucket is 45 cm and the radii of its top and bottom are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the surface area of the solid.
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
The surface area of a sphere is 616 cm2. Its radius is ______.
Four horses are tethered with equal ropes at 4 corners of a square field of side 70 metres so that they just can reach one another. Find the area left ungrazed by the horses.
