Advertisements
Advertisements
Question
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
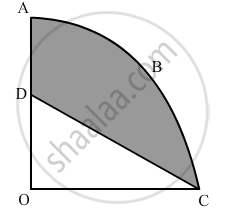
Solution
Area of the quadrant OABC\[= \frac{1}{4} \times \pi r^2\]\[= \left( \frac{1}{4} \times \frac{22}{7} \times 7 \times 7 \right) {cm}^2 \]
\[ = \frac{77}{2} {cm}^2\]
Area of ΔODC\[=\]\[\frac{1}{2} \times OD \times OC\]
\[= \left( \frac{1}{2} \times 4 \times 7 \right) {cm}^2 ( \because \text{OC is the radius of the circle})\]
\[ = 14 {cm}^2\]
Area of the shaded region = Area of the quadrant OABC − Area of ΔODC
\[= \frac{77}{2} {cm}^2 - 14 {cm}^2 \]
\[ = \frac{77 - 28}{2} {cm}^2 \]
\[ = \frac{49}{2} {cm}^2 \]
\[ = 24 . 5 {cm}^2 \]
APPEARS IN
RELATED QUESTIONS
The dimensions of a solid iron cuboid are 4·4 m × 2·6 m × 1·0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond ?
A hollow sphere of internal and external diameters 4 and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Height of a solid cylinder is 10 cm and diameter 8 cm. Two equal conical hole have been made from its both ends. If the diameter of the holes is 6 cm and height 4 cm, find (i) volume of the cylinder, (ii) volume of one conical hole, (iii) volume of the remaining solid.
A cylindrical vessel of radius 4 cm contains water. A solid sphere of radius 3 cm is lowered into the water until it is completely immersed. The water level in the vessel will rise by
Water is flowing at the rate of 6 km/hr through a pipe of diameter 14 cm into a rectangular tank which is 60 m long and 22 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
If R is the radius of the base of the hat, then the total outer surface area of the hat is ______.

