Advertisements
Advertisements
Question
A hollow sphere of internal and external diameters 4 and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Solution
Internal radius of hemisphere `r_1 = 4/2`= 2 cm
External radius of hemisphere `r_2 = 8/2`= 4 cm
Volume of hollow sphere `= 4/3 pi (r_2^3 - r_1^3)`
` = 4/3 pi (64 - 8)`
`= 4/3 pi xx 56`
`= (224)/3 pi cm^2`
Since,
The hemisphere melted into a cone of radius r = 4 cm
Let h be height of the cone.
Clearly, the volume of cone = volume of hemisphere
`1/3pi(4)^2 xx h = (224)/3 pi`
`h = (224)/6`
`h = 14`
Thus, the height is 14 cm.
APPEARS IN
RELATED QUESTIONS
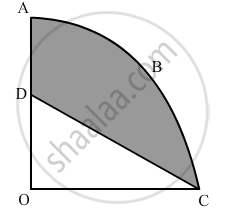
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
If the radii of the circular ends of a bucket of height 40 cm are of lengths 35 cm and 14 cm, then the volume of the bucket in cubic centimeters, is
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 98 cm and the diameter of each of its hemispherical ends is 28 cm, find the cost of polishing the surface of the solid at the rate of 15 paise per sq cm.
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
Find the number of solid spheres, each of diameter 6 cm, that could be moulded to form a solid metallic cylinder of height 45 cm and diameter 4 cm.
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
If the length of the diagonal of a cube is `5sqrt(3)` cm, find the total surface area.
Length of the diagonal of the cube = `square`
So, `square` = `5sqrt(3)`
⇒ Side = `square`
Total surface area of cube = `square`
= `square` × `square` × `square`
= `square` cm2
Hence, the total surface area is `square`.
