Advertisements
Advertisements
Question
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Solution
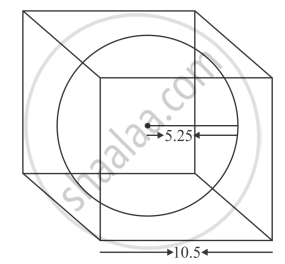
The side of cube a = 10.5 cm.
Since, a largest sphere is curved out of that cube
i.e., radius of sphere,
`r = a/2`
`r= (10.5)/2 cm`
`r = 5.25 cm`
The volume of sphere
`= 4/3 pi (5.25)^3`
`=4/3 xx 22/7 xx 5.25 xx 5.25 xx 5.25`
` = 22 xx 0.75 xx 1.75 xx 21`
` = 606.375 cm^3`
APPEARS IN
RELATED QUESTIONS
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter 5 cm and height 6 cm. How many bottles are necessary to empty the bowl?
The radii of two cylinders are in the ratio 3 : 5 and their heights are in the ratio 2 : 3. What is the ratio of their curved surface areas?
If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, the diameter of the sphere is
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
Two cubes, each of volume 64 cm3, are joined end to end. Find the total surface area of the resulting cuboid.
Arrange the given objects according to their volume
The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
