Advertisements
Advertisements
Question
A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter 5 cm and height 6 cm. How many bottles are necessary to empty the bowl?
Solution
Internal radius of hemispherical bowl r = 15 cm
The volume of bowl `= 2/3 pir^3`= volume of liquid
`= 2/3 pi(15)^3`
Volume of liquid = 2250 π cm3
Since, the liquid filled into the cylindrical shaped bottles of radius `5/2 cm`and height 6 cm.
Let n be the no. of bottles.
Therefore,
The volume of liquid = n × volume of cylindrical shaped bottle
`2250pi = n xx pi xx (5/2)^2 xx 6`
`2250 = n xx 25 / 4 xx 6`
`n = (2250 xx 4)/(25 xx 6)`
` n = 60`
Hence, the no. of bottles = 60
APPEARS IN
RELATED QUESTIONS
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
The dimensions of a solid iron cuboid are 4·4 m × 2·6 m × 1·0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
The curved surface area of a cylinder is 264 m2 and its volume is 924 m3. The ratio of its diameter to its height is
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
The surface areas of two spheres are in the ratio of 4 : 25. Find the ratio of their volumes.
The ratio between the volume of two spheres is 8 : 27. What is the ratio between their surface areas?
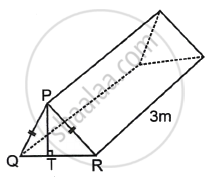
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent