Advertisements
Advertisements
Question
In a cylindrical vessel of diameter 24 cm, filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Find the increase in height of water level.
Solution
Radius of spherical ball r = 6 cm, radius of cylindrical vessel r1 = 12 cm
Since, the ball completely immersed into the vessel, the water level is increased.
Let the height of increased level.
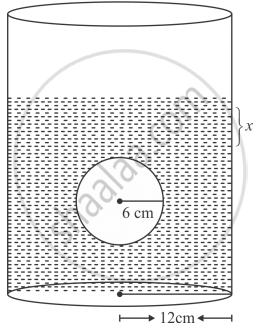
Therefore,
The volume of increase water level = volume of ball
`pi xx (12)^2 xx x = 4/3 pi xx (6)^3`
`144 x = 4/3 xx 216`
`144x = 4 xx 72`
`x = (4 xx 72)/144`
x = 2 cm
Hence, the level of water increased by 2 cm.
APPEARS IN
RELATED QUESTIONS
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/12 cm, find the length of the wire.
Two cones have their heights in the ratio 1 : 3 and radii 3 : 1. What is the ratio of their volumes?
A cylindrical vessel of radius 4 cm contains water. A solid sphere of radius 3 cm is lowered into the water until it is completely immersed. The water level in the vessel will rise by
The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 km2. Find the height of the mountain.
The radii of the circular ends of a bucket of height 15 cm are 14 cm and r cm (r < 14). If the volume of bucket is 5390 cm3, then find the value of r.
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
Find the surface area of a sphere of radius 3.5 cm.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
A sphere and a cube have equal surface areas. The ratio of the volume of the sphere to that of cube is ______.
______ of a solid is the measurement of the space occupied by it.
