Advertisements
Advertisements
प्रश्न
In a cylindrical vessel of diameter 24 cm, filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Find the increase in height of water level.
उत्तर
Radius of spherical ball r = 6 cm, radius of cylindrical vessel r1 = 12 cm
Since, the ball completely immersed into the vessel, the water level is increased.
Let the height of increased level.
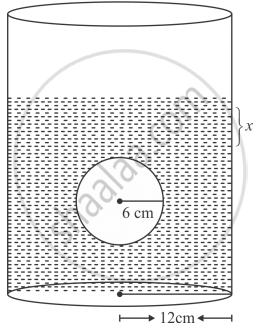
Therefore,
The volume of increase water level = volume of ball
`pi xx (12)^2 xx x = 4/3 pi xx (6)^3`
`144 x = 4/3 xx 216`
`144x = 4 xx 72`
`x = (4 xx 72)/144`
x = 2 cm
Hence, the level of water increased by 2 cm.
APPEARS IN
संबंधित प्रश्न
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
A pen stand made of wood is in the shape of a cuboid with four conical depression and a cubical depression to hold the pens and pins , respectively . The dimension of the cuboid are \[10 cm \times 5 cm \times 4 cm\].
The radius of each of the conical depression is 0.5 cm and the depth is 2.1 cm . The edge of the cubical depression is 3 cm . Find the volume of the wood in the entire stand.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
The radii of the circular ends of a bucket of height 15 cm are 14 cm and r cm (r < 14). If the volume of bucket is 5390 cm3, then find the value of r.
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
How many solid cylinders of radius 6 cm and height 12 cm can be made by melting a solid sphere of radius 18 cm?
Activity: Radius of the sphere, r = 18 cm
For cylinder, radius R = 6 cm, height H = 12 cm
∴ Number of cylinders can be made =`"Volume of the sphere"/square`
`= (4/3 pir^3)/square`
`= (4/3 xx 18 xx 18 xx 18)/square`
= `square`
A surahi is the combination of ______.
______ surface area of room = area of 4 walls.
The radius of a metallic sphere is 8 cm. It was melted to make a wire of diameter 6 mm. Find the length of the wire.
