Advertisements
Advertisements
Question
Find the surface area of a sphere of radius 3.5 cm.
Solution
Radius (r) of sphere = 3.5 cm
∴ Surface area = 4πr2
`= 4 xx 22/7 xx 3.5 xx 3.5`
`= 88 xx 1.75`
= 154 cm2
APPEARS IN
RELATED QUESTIONS
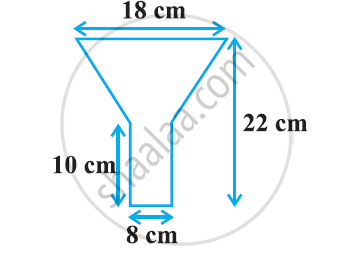
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
A solid metallic sphere of diamter 16 cm is melted and recasted into smaller solid cones, each of radius 4 cm and height 8 cm. Find the number of cones so formed.
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is `14/3` m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is ______.
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of Rs. 10 per sq.m.
A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and contains \[41\frac{19}{21} m^3\] of air. If the internal diameter of dome is equal to its total height above the floor , find the height of the building ?
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use : π = 355/115)
If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, the diameter of the sphere is
A hemispherical bowl of internal radius 9 cm is full of water. Its contents are emptied into a cylindrical vessel of internal radius 6 cm. Find the height of water in the cylindrical vessel.
If the area of the base of a right circular cone is 3850 cm2 and its height is 84 cm, then find the slant height of the cone.
The curved surface are of a cylinder is 1760 cm2 and its base radius is 14 cm. The height of the cylinder is
The ratio between the volume of two spheres is 8 : 27. What is the ratio between their surface areas?
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
From a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. (Use π = 3.14)
In a right circular cone, if the perpendicular height is 12 cm and the radius is 5 cm, then find its slant height.
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is ______.
______ of a solid is the measurement of the space occupied by it.
A rectangular examination hall having seats for 500 candidates has to be built so as to allow 4 cubic metres of air and 0.5 square metres of floor area per candidate. If the length of hall be 25 m, find the height and breadth of the hall.
