Advertisements
Advertisements
प्रश्न
Find the surface area of a sphere of radius 3.5 cm.
उत्तर
Radius (r) of sphere = 3.5 cm
∴ Surface area = 4πr2
`= 4 xx 22/7 xx 3.5 xx 3.5`
`= 88 xx 1.75`
= 154 cm2
APPEARS IN
संबंधित प्रश्न
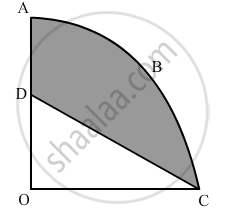
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
In the middle of a rectangular field measuring 30 m × 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
The vertical height of a conical tent is 42 dm and the diameter of its base is 5.4 m. Find the number of persons it can accommodate if each person is to be allowed 29.16 cubic dm.
A wall 24 m , 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm \[\times\] 16 cm \[\times\] 10 cm . If the mortar occupies \[\frac{1}{10}th\] of the volume of the wall, then find the number of bricks used in constructing the wall.
Two cones have their heights in the ratio 1 : 3 and radii 3 : 1. What is the ratio of their volumes?
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, the radius of its base is
The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 km2. Find the height of the mountain.
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
Water is flowing at the rate of 6 km/hr through a pipe of diameter 14 cm into a rectangular tank which is 60 m long and 22 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
In a corner of a rectangular field with dimensions 35m × 22 m, a well with 14 m inside diameter is dug 8 m deep. The earth dug out is spread evenly over the remaining part of the field. Find the rise in the level of the field.
If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, then find its capacity and total surface area.
A sphere of diameter 18 cm is dropped into a cylindrical vessel of diameter 36 cm, partly filled with water. If the sphere is completely submerged, then the water level rises by ______.
Choose the correct answer of the following question:
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The sum of length, breadth and height of a cuboid is 19 cm and its diagonal is `5sqrt(5)` cm. Its surface area is
The ratio of the total surface area to the lateral surface area of a cylinder with base radius 80 cm and height 20 cm is
Assertion (A)
If the radii of the circular ends of a bucket 24 cm high are 15 cm and 5 cm, respectively, then the surface area of the bucket is 545π cm2.
- Reason(R)
If the radii of the circular ends of the frustum of a cone are R and r, respectively, and its height is h, then its surface area is - Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
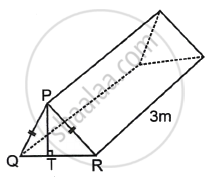
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent