Advertisements
Advertisements
Question
In a right circular cone, if the perpendicular height is 12 cm and the radius is 5 cm, then find its slant height.
Solution
Heights (h) = 12 cm
Radius (r) = 5 cm
∴ Slant height (l) = `sqrt (h^2 + r^2)`
= `sqrt(12^2 + 5^2)`
= `sqrt(144 + 25)`
= `sqrt(169)`
= 13 cm
∴ l = 13 cm
APPEARS IN
RELATED QUESTIONS
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
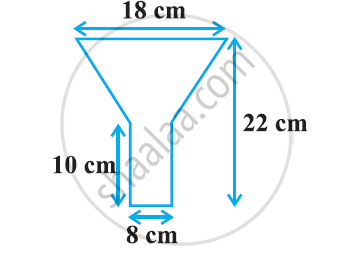
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
The dimensions of a solid iron cuboid are 4·4 m × 2·6 m × 1·0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is `14/3` m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere ?
Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in level of water in the tank in half an hour ?
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
Two cubes have their volumes in the ratio 1 : 27. What is the ratio of their surface areas?
If the volumes of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5, then write the ratio of their weights.
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
If the area of the base of a right circular cone is 3850 cm2 and its height is 84 cm, then find the slant height of the cone.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If its volume is 1617 cm3, the total surface area of the cylinder is
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
Arrange the given objects according to their volume
A factory manufactures 120000 pencils daily. The pencils are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm. Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at Rs 0.05 per dm2.
