Advertisements
Advertisements
Question
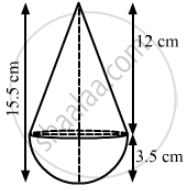
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
Solution
We have,
Radius of the hemisphere = Radius of the cone = r = 3.5 cm and
Height of the cone = 15.5 - 3.5 = 12 cm
Also,
The slant height of the cone,` "l" = sqrt("h"^2 +"r"^2)`'
`= sqrt(12^2+3.5^2)`
`=sqrt(144+12.25)`
`=sqrt(156.25)`
=12.5 cm
Now,
Total surface area of the toy = CSA of cone + CSA of hemisphere
`=pi"rl" + 2pi"r"^2`
`=pir("l"+2"r")`
`=22/7xx3.5xx(12.5+2xx3.5)`
`=11xx(12.5 + 7)`
`=11xx19.5`
=214.5 cm2
So, the total surface area of the toy is 214.5 cm2.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
RELATED QUESTIONS
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 `5/9` cm. Find the diameter of the cylindrical vessel.
A factory manufactures 120,000 pencils daily . The pencil are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm . Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm2.
A spherical ball of iron has been melted and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m × 16 m × 11 m.
Two cubes have their volumes in the ratio 1 : 27. What is the ratio of their surface areas?
A shuttlecock used for playing badminton is a combination of

The ratio of the total surface area to the lateral surface area of a cylinder with base radius 80 cm and height 20 cm is
The curved surface are of a cylinder is 1760 cm2 and its base radius is 14 cm. The height of the cylinder is
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
Arrange the given objects according to their volume
