Advertisements
Advertisements
प्रश्न
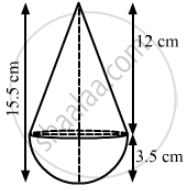
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
उत्तर
We have,
Radius of the hemisphere = Radius of the cone = r = 3.5 cm and
Height of the cone = 15.5 - 3.5 = 12 cm
Also,
The slant height of the cone,` "l" = sqrt("h"^2 +"r"^2)`'
`= sqrt(12^2+3.5^2)`
`=sqrt(144+12.25)`
`=sqrt(156.25)`
=12.5 cm
Now,
Total surface area of the toy = CSA of cone + CSA of hemisphere
`=pi"rl" + 2pi"r"^2`
`=pir("l"+2"r")`
`=22/7xx3.5xx(12.5+2xx3.5)`
`=11xx(12.5 + 7)`
`=11xx19.5`
=214.5 cm2
So, the total surface area of the toy is 214.5 cm2.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
संबंधित प्रश्न
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2 : 3.
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm. find the number of lead spheres dropped in the water.
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
Assertion (A)
The outer surface of a hemisphere of radius 7 cm is to be painted. The total cost of painting at Rs 5 per cm2 is Rs 2300.
Reason (R)
The total surface area of a hemisphere is 3π r2.
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
From a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. (Use π = 3.14)
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.