Advertisements
Advertisements
प्रश्न
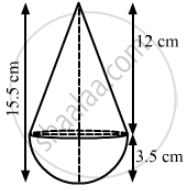
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
उत्तर
We have,
Radius of the hemisphere = Radius of the cone = r = 3.5 cm and
Height of the cone = 15.5 - 3.5 = 12 cm
Also,
The slant height of the cone,` "l" = sqrt("h"^2 +"r"^2)`'
`= sqrt(12^2+3.5^2)`
`=sqrt(144+12.25)`
`=sqrt(156.25)`
=12.5 cm
Now,
Total surface area of the toy = CSA of cone + CSA of hemisphere
`=pi"rl" + 2pi"r"^2`
`=pir("l"+2"r")`
`=22/7xx3.5xx(12.5+2xx3.5)`
`=11xx(12.5 + 7)`
`=11xx19.5`
=214.5 cm2
So, the total surface area of the toy is 214.5 cm2.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
संबंधित प्रश्न
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
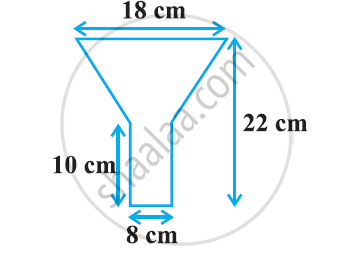
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
A solid sphere of diameter 6 cm is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
A solid metallic spherical ball of diameter 6 cm is melted and recast into a cone with diameter of the base as 12 cm. The height of the cone is
The rain water from a roof of 44 m × 20 m drains into a cylindrical tank having diameter of base 4 m and height 3.5 m. If the tank is just full, then find the rainfall in cm.
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
The surface area of a sphere is 154 cm2. The volume of the sphere is
Two cubes, each of volume 64 cm3, are joined end to end. Find the total surface area of the resulting cuboid.
A sphere and a cube have equal surface areas. The ratio of the volume of the sphere to that of cube is ______.
