Advertisements
Advertisements
प्रश्न
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
उत्तर
Radius of the cone, r = 1.5 cm
Height of the cone, h = 5 cm
∴ Volume of the cone, V = \[\frac{1}{3}\pi r^2 h = \frac{1}{3} \times \frac{22}{7} \times \left( 1 . 5 \right)^2 \times 5 =\] 11.79 cm3
Thus, the volume of the cone is 11.79 cm3.
APPEARS IN
संबंधित प्रश्न
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 `5/9` cm. Find the diameter of the cylindrical vessel.
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
The dimensions of a solid iron cuboid are 4·4 m × 2·6 m × 1·0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe
The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of Rs. 10 per sq.m.
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
The vertical height of a conical tent is 42 dm and the diameter of its base is 5.4 m. Find the number of persons it can accommodate if each person is to be allowed 29.16 cubic dm.
A golf ball has diameter equal to 4.2 cm. Its surface has 200 dimples each of radius 2 mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4, what is the ratio of their volumes?
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii ?
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
Water flows at the rate of 10 metre per minute from a cylindrical pipe 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder. The diameter of the hemisphere is 21 cm and the total height of the vessel is 14.5 cm. Find its capacity.
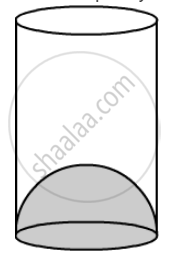
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
Three cubes of iron whose edges are 6 cm, 8 cm and 10 cm, respectively are melted and formed into a single cube. Find the edge of the new cube formed.
The surface areas of two spheres are in the ratio of 4 : 25. Find the ratio of their volumes.
Two cubes, each of volume 64 cm3, are joined end to end. Find the total surface area of the resulting cuboid.
If the side of a cube is 5 cm, then find its volume.
