Question

A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.

Answer 1

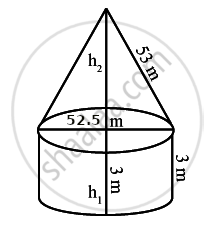
Given,
Height of cylinder (h) = 3 m
Base radius of cylinder (r) = 52.5 m
Slant height of cone (l) = 53 m
Base radius of cone = Base radius of cylinder (r) = 52.5 m

∴ Area of canvas needed = Curved surface area of the cylindrical portion + Curved surface area of the conical portion

∴ Area of canvas needed =  πrl + 2πrh

∴ Area of canvas needed = πr(l + 2h)

∴ Area of canvas needed = (`22/7` × 52.5)(53 + 2 × 3)

∴ Area of canvas needed = `22/7` × 52.5 × 59

∴ Area of canvas needed = 9735 m²