Advertisements
Advertisements
प्रश्न
A hemispherical bowl of internal radius 9 cm is full of water. Its contents are emptied in a cylindrical vessel of internal radius 6 cm. Find the height of water in the cylindrical vessel.
उत्तर
Let the height of water in the cylindrical vessel be h cm.
Given: Radius of the hemispherical bowl, r = 9 cm
∴ Volume of the water in hemispherical bowl, `V_1=pi2/3r^3`
`V_1=pi2/3xx(9cm)`
Given: Radius of the cylinder, R = 6 cm,
∴ Volume of water in the cylindrical vessel, V2 = π r2h
⇒ V2 = π (6 cm)2 h
Since water is emptied from the hemispherical bowl into the cylindrical vessel,
∴Volume of water in cylindrical vessel = Volume of the water in hemispherical bowl
`rArrpi(6)^2h=2/3pi(9)^3`
`rArrh=(2xx(9)^3)/(3xx(6)^2)`
`rArrh=27/2`
`rArrh=13.5`
Thus, the height of water in the cylindrical vessel is 13.5 cm.
APPEARS IN
संबंधित प्रश्न
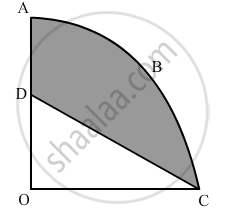
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/hr. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired ?
Two cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
The diameter of a cylinder is 28 cm and its height is 20 cm. The total surface area of the cylinder is
The surface areas of a sphere and a cube are equal. Find the ratio of their volumes.
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
Arrange the given objects according to their volume
______ of a solid is the measurement of the space occupied by it.
