Advertisements
Advertisements
प्रश्न
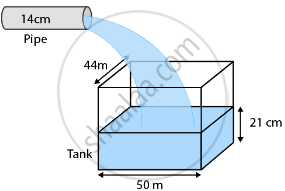
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
उत्तर १
Speed at which the water is flowing through the pipe = 15 km / h = `(15000m)/(3600s)=25/6 m/s`
Radius of the pipe= `(14cm)/2=7cm=7/100m`
Length of the cuboidal pond = 50 m
Breadth of the cuboidal pond = 44 m
Rise in the level of water in the pond =21 cm = `21/100m`
Time (in sec) taken by the pipe to fill the pond
`\text{Volume of the pond}/\text{Volume of the water flowing through the4 pipe in 1 second}`
`=(50m xx44mxx21/100m)/(22/7xx7/100mxx7/100mxx25/6m)s`
`=7200 s`
`=7200/3600h`
`=2h`
Thus, the time taken by the pipe to fill the pond is 2 hours.
उत्तर २
Let the time taken by pipe to fill pond = t hours
Water flows 15 km in 1 hour,
So it will flow 15t meters in t hours.
We know that,
Volume of cuboidal pond up to height 21 cm = Volume of water that passes through pipe in “t” hours
Considering cuboidal pond,
Length, l = 50 m
Breadth, b = 44 m
Height, h = 21 cm = 0.21 m
We know that,
Volume of tank = lbh
Volume of water = 50(44)(0.21) = 462 m3
Considering cylindrical pipe
Base diameter = 14 cm
Base radius, r = 7 cm = 0.07 m
Height, h = 15t km = 15000t m
We also know that,
Volume of a cylinder = πr2h
Volume of water passed in pipe = π(0.07)2(15000t)
= `22/7 xx 0.07 xx 0.07 xx 15000"t"`
= 231t cm3
So, we have
231t = 462
t = 2 hours
Time required to fill tank up to a height of 25 cm is 2 hours.
संबंधित प्रश्न
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/12 cm, find the length of the wire.
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is ______.
A metal parallelopiped of measures 16 cm x 11 cm x 10 cm was melted to make coins. How many coins were made if the thickness and diameter of each coin were 2 mm and 2 cm respectively?
The vertical height of a conical tent is 42 dm and the diameter of its base is 5.4 m. Find the number of persons it can accommodate if each person is to be allowed 29.16 cubic dm.
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm. find the number of lead spheres dropped in the water.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
If the side of a cube is 5 cm, then find its volume.
The surface area of a sphere is 616 cm2. Its radius is ______.
A bicycle wheel makes 500 revolutions in moving 1 km. Find the diameter of the wheel.
