Question

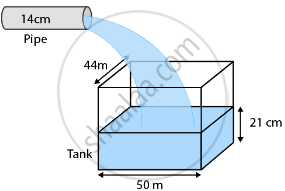
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?

Answer 1

Speed at which the water is flowing through the pipe = 15 km / h = `(15000m)/(3600s)=25/6 m/s`

Radius of the pipe= `(14cm)/2=7cm=7/100m`

Length of the cuboidal pond = 50 m

Breadth of the cuboidal pond = 44 m

Rise in the level of water in the pond =21 cm = `21/100m`

Time (in sec) taken by the pipe to fill the pond

`\text{Volume of the pond}/\text{Volume of the  water flowing through the4 pipe in 1 second}`

`=(50m xx44mxx21/100m)/(22/7xx7/100mxx7/100mxx25/6m)s`

`=7200 s`

`=7200/3600h`

`=2h`

Thus, the time taken by the pipe to fill the pond is 2 hours.

Answer 2

Let the time taken by pipe to fill pond = t hours

Water flows 15 km in 1 hour,

So it will flow 15t meters in t hours.

We know that,

Volume of cuboidal pond up to height 21 cm = Volume of water that passes through pipe in “t” hours

Considering cuboidal pond,

Length, l = 50 m

Breadth, b = 44 m

Height, h = 21 cm = 0.21 m

We know that,

Volume of tank = lbh

Volume of water = 50(44)(0.21) = 462 m³

Considering cylindrical pipe

Base diameter = 14 cm

Base radius, r = 7 cm = 0.07 m

Height, h = 15t km = 15000t m

We also know that,

Volume of a cylinder = πr²h

Volume of water passed in pipe = π(0.07)²(15000t)

= `22/7 xx 0.07 xx 0.07 xx 15000"t"`

= 231t cm³

So, we have

231t = 462

t = 2 hours

Time required to fill tank up to a height of 25 cm is 2 hours.