Advertisements
Advertisements
Question
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of canvas used in making the tent, if the breadth of the canvas is 1.5 m.
Solution
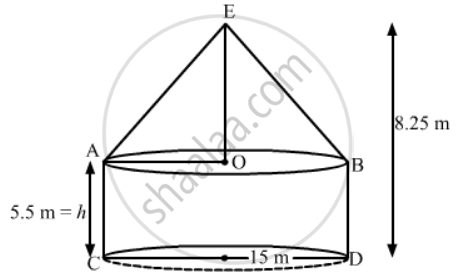
We have,
the radii of bases of the cone and cylinder, r = 15 m,
the height of the cylinder, h = 5.5 m,
the height of the tent = 8.25 m
Also, the height of the cone, H = 8.25 - 5.5 = 2.75 m
The slant height of the cone, l = `sqrt(r^2 + H^2)`
`= sqrt(15^2 + 2.75^2)`
`= sqrt(225 + 7.5625)`
`= sqrt(232.5625)`
`= 15.25` m
The area of the canvas used in making the tent = CSA of cylinder + CSA of cone
= 2πrh + πrl
= πr(2h + l)
`= 22/7 xx15 (2xx5.5+15.25)`
`=22/7xx 15(11 + 15.25)`
`=22/7 xx15xx26.25`
= 1237.5 m2
As, the width of the canvas = 1.5 m
So, the length of the canvas =`237.5/1.5 = 825` m
Hence, the length of the tent used for making the tent is 825 m.
APPEARS IN
RELATED QUESTIONS
The `3/4` th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
Find the ratio of the volumes of a cylinder and a cone having equal radius and equal height.
(A)1 : 2 (B) 2 : 1 (C) 1 : 3 (D) 3 : 1
A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and contains \[41\frac{19}{21} m^3\] of air. If the internal diameter of dome is equal to its total height above the floor , find the height of the building ?
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1m3 of metal weighs 21g.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the surface area of the solid.
Find the surface area of a sphere of radius 3.5 cm.

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
The capacity of a closed cylindrical vessel of height 1 m is 15.4 L. How many square metres of metal sheet would be needed to make it?
