Advertisements
Advertisements
प्रश्न
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of canvas used in making the tent, if the breadth of the canvas is 1.5 m.
उत्तर
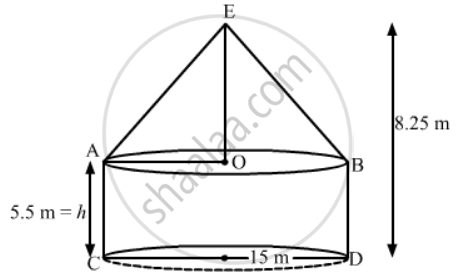
We have,
the radii of bases of the cone and cylinder, r = 15 m,
the height of the cylinder, h = 5.5 m,
the height of the tent = 8.25 m
Also, the height of the cone, H = 8.25 - 5.5 = 2.75 m
The slant height of the cone, l = `sqrt(r^2 + H^2)`
`= sqrt(15^2 + 2.75^2)`
`= sqrt(225 + 7.5625)`
`= sqrt(232.5625)`
`= 15.25` m
The area of the canvas used in making the tent = CSA of cylinder + CSA of cone
= 2πrh + πrl
= πr(2h + l)
`= 22/7 xx15 (2xx5.5+15.25)`
`=22/7xx 15(11 + 15.25)`
`=22/7 xx15xx26.25`
= 1237.5 m2
As, the width of the canvas = 1.5 m
So, the length of the canvas =`237.5/1.5 = 825` m
Hence, the length of the tent used for making the tent is 825 m.
APPEARS IN
संबंधित प्रश्न
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
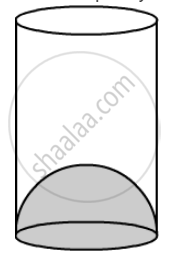
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
The surface areas of two spheres are in the ratio of 4 : 25. Find the ratio of their volumes.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The diameter of a cylinder is 28 cm and its height is 20 cm. The total surface area of the cylinder is
The ratio of the total surface area to the lateral surface area of a cylinder with base radius 80 cm and height 20 cm is
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
Find the surface area of a sphere of radius 3.5 cm.

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
