Advertisements
Advertisements
प्रश्न
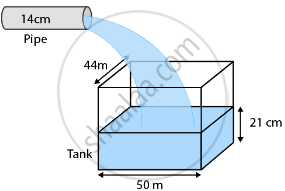
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
उत्तर १
Speed at which the water is flowing through the pipe = 15 km / h = `(15000m)/(3600s)=25/6 m/s`
Radius of the pipe= `(14cm)/2=7cm=7/100m`
Length of the cuboidal pond = 50 m
Breadth of the cuboidal pond = 44 m
Rise in the level of water in the pond =21 cm = `21/100m`
Time (in sec) taken by the pipe to fill the pond
`\text{Volume of the pond}/\text{Volume of the water flowing through the4 pipe in 1 second}`
`=(50m xx44mxx21/100m)/(22/7xx7/100mxx7/100mxx25/6m)s`
`=7200 s`
`=7200/3600h`
`=2h`
Thus, the time taken by the pipe to fill the pond is 2 hours.
उत्तर २
Let the time taken by pipe to fill pond = t hours
Water flows 15 km in 1 hour,
So it will flow 15t meters in t hours.
We know that,
Volume of cuboidal pond up to height 21 cm = Volume of water that passes through pipe in “t” hours
Considering cuboidal pond,
Length, l = 50 m
Breadth, b = 44 m
Height, h = 21 cm = 0.21 m
We know that,
Volume of tank = lbh
Volume of water = 50(44)(0.21) = 462 m3
Considering cylindrical pipe
Base diameter = 14 cm
Base radius, r = 7 cm = 0.07 m
Height, h = 15t km = 15000t m
We also know that,
Volume of a cylinder = πr2h
Volume of water passed in pipe = π(0.07)2(15000t)
= `22/7 xx 0.07 xx 0.07 xx 15000"t"`
= 231t cm3
So, we have
231t = 462
t = 2 hours
Time required to fill tank up to a height of 25 cm is 2 hours.
संबंधित प्रश्न
To fill a swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool.
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm. find the number of lead spheres dropped in the water.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
The surface area of a sphere is same as the curved surface area of a right circular cylinder whose height and diameter are 12 cm each. The radius of the sphere is
A sphere of diameter 18 cm is dropped into a cylindrical vessel of diameter 36 cm, partly filled with water. If the sphere is completely submerged, then the water level rises by ______.
The total surface area of a cube is 864 cm2. Its volume is
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
