Advertisements
Advertisements
प्रश्न
A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
उत्तर
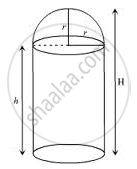
Let the radius of the dome be r.
Diameter be d.
Let the height of the building be H.
Given \[d = \frac{2}{3}H\]
\[\Rightarrow 2r = \frac{2}{3}H\]
\[ \Rightarrow r = \frac{H}{3}\]
\[ \Rightarrow 3r = H\]
Also, h + r = H
\[\Rightarrow 3r = h + r\]
\[ \Rightarrow 2r = h\]
\[ \Rightarrow r = \frac{h}{2}\]
Volume of air = Volume of air in the cylinder + Volume of air int he hemispherical dome
\[\Rightarrow \pi r^2 h + \frac{2}{3} \pi r^3 = 67\frac{1}{21}\]
\[ \Rightarrow \pi \left( \frac{h}{2} \right)^2 h + \frac{2}{3}\pi \left( \frac{h}{2} \right)^3 = \frac{1408}{21}\]
\[ \Rightarrow h^3 = \frac{11264}{176} = 64\]
\[ \Rightarrow h = 4 m\]
Hence, the radius will be \[r = \frac{h}{2} = \frac{4}{2} = 2 m\]
Height of the building, H = 3r = \[3 \times 2 = 6 m\]
APPEARS IN
संबंधित प्रश्न
Find the volume of a sphere of diameter 6 cm.
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, determine the ratio of the radius of the base to the height of either of them.
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1m3 of metal weighs 21g.
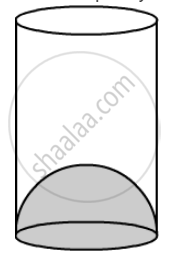
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
66 cubic cm of silver is drawn into a wire 1 mm in diameter. Calculate the length of the wire in metres.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total
surface area of the toy.
A shuttlecock used for playing badminton is a combination of


In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
The shape of a gilli, in the gilli-danda game (see Fig.), is a combination of ______.

